The Vocabulary of Subtraction

Near the beginning of this month, there was a blog entry (“Vocabulary of Addition”) in which I defined the math terms for an equation using the operation of addition. Today, I will show you the English math words associated with the fundamental skill of subtraction and its associated numerical expressions {language model}.

A minuend is the number from which another is to be subtracted.

The minus sign is the symbol that represents the operation of subtraction in this equation.

The subtrahend is the number to be subtracted from the minuend.

The difference is the result of subtracting the subtrahend from the minuend.

As you can see, the terms associated with subtraction are a little more obscure and less commonly used in math conversations than the ones for addition. These terms emphasize the fact that the order of terms in subtracting two numbers does matter.  We need to recognize this difference when we use language to describe mathematics.

The Equality of Robert Recorde

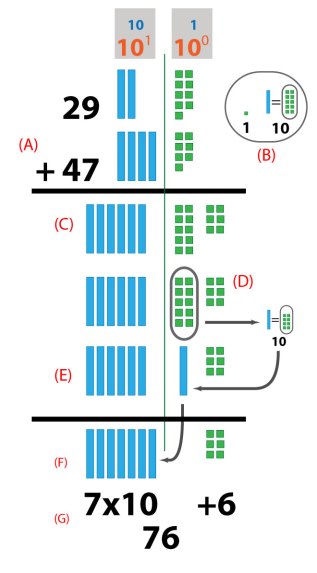
Throughout their education, students will come across the most ubiquitous symbol in all of mathematics. It’s the symbol that defines all equations. It is the equal sign.  But where did it come from?

Robert Recorde (ca. 1512-1558) was a Welsh physician and mathematician. At the age of fifteen, he entered Oxford University, graduating in 1531. In the same year he was elected a Fellow of All Souls College. Moving to Cambridge University he obtained a degree in medicine in 1545. He is known as the founder of the English School of Mathematics and was the first person to write mathematical books in English. He also introduced, among other things, the idea of placing two hyphens in parallel to symbolize the balance of two expressions in a mathematical equation.

He wrote a math textbook with a most convoluted title: “The Whetstone of Witte, whiche is the seconde parte of Arithmeteke: containing the extraction of rootes; the cossike practise, with the rule of equation; and the workes of Surde Nombers” (Published in 1557). You can find and download a digitized version of this textbook here at the Internet Archive. The book covers topics including whole numbers, the extraction of roots and irrational numbers as well as the execution of arithmetic operations.

This is the page in which he defines the familiar symbol:

“And to avoide the tedious repetition of these woordes: is equalle to: I will sette as I doe often in woorke use, a paire of paralleles, or gemowe lines of one length, thus: =, because noe. 2. thynges, can be moare equalle.”

He uses this symbol to subsequently express numerous equations, beginning at the bottom of this page. Thus, it can be said that the first math equation to be expressed using this modern notation is 14x + 15 = 71. Thankfully, by the time this symbol was consistently used in the 1700s, the two parallel lines (as well as other symbols he defined) were made more compact.

Robert Recorde is honored with a wall tablet at St. Mary’s Church. It is located in his birth town of Tenby, Pembrokeshire, Wales. It documents his achievements to mathematics:

“To his genius we owe the earliest important English treatises on algebra, arithmetic, astronomy, and geometry: He also invented the sign of equality, =, now universally adopted by the civilized world.”

There is also a display at the Tenby Museum & Art Gallery documenting the achievements of this Welsh mathematical pioneer.

Explore and enjoy!

The Standard Algorithm of Addition: Part 3

In the blog “Standard Algorithm of Addition: Part 1,” we learned how to set up addition problems in a vertical format so that we can manually calculate their sum. We also learned the mathematical terms for the components of arithmetic expressions of additions. In the blog “Standard Algorithm of Addition: Part 2,” I used a {visual model} to explain the concept behind this fundamental algorithm using green square blocks and blue rods to represent the addends. In this blog, I will show you how the standard algorithm works {number model}.

First we set up the arithmetic expression in a vertical format (A). Now we will first focus on the ones column and work our way from right to left (B). We mentally add the digits in the ones (9+7=16). Note the sum is greater than 9. This sum is equivalent to 1 unit of ten (blue rod) and 6 units of ones (green squares) (C). I write the digit for the 6 units of one in the ones column under the underline (D). I place the 1 digit of ten at the top of the tens column (E).

Working our way from right to left, we move to the tens column (F). We add the digits in this column noting that we are actually adding multiples of ten (G). Since the sum is not greater than 99, we simply write the sum of the digits in the tens column underneath the underline (H). Therefore, the sum of the addends, 29 and 47, is 76 (I).  It is the most common technique of addition taught to math students, but it is not the only one.  We’ll look at some other addition algorithms in future blogs.

Standard Algorithm of Addition: Part 2

I believe that math students of all ages learn abstract notions by first experiencing them concretely with shapes they can actually see, touch and manipulate {visual model}. we will use of concrete teaching aids such as base-ten blocks help provide insight into the creation of the standard algorithm for addition. In this blog, we will use them to find the sum of two whole numbers, 29 and 47 (A). I will be using two types of blocks (B). A green square block has a value of 1 unit, and a blue rod has a value of 10 units. I represent the values of the two addends using these two blocks. I make sure that they are grouped in the appropriate columns according to the structure of the decimal number system (See “Decimals”). I then add all the blue rods together in the tens column, and add all the green squares together in the ones column (C). Notice that we have more than ten green squares. I group ten of these squares together (D) and replace them with a blue rod (E). This blue rod gets moved from the ones column to the tens column (F). Now we have seven blue rods and six green squares, which represent the sum: 76 (G).

We can use these two blocks to visually add numbers 1-99. Additional blocks can be added that represent larger multiples of 10 so that larger whole numbers can be used.

Standard Algorithm of Addition: Part I

As part of our primary education in mathematics, we have all been taught a standard method for adding two or more numbers together. Students learn how to add a series of whole numbers by following a step-by-step process until they can apply it without making an error. As part of the math education, it is also important that math students understand why this step-by-step process, the standard algorithm of addition, works.

First we need to set up our arithmetic expression of addition properly {number model}. In the blog, “The Vocabulary of Addition,” we learned the math terms for the different components of arithmetic expressions and equations involving addition. In that blog, the arithmetic expression and equation was presented in a horizontal format. Such expressions and equations can also be presented in a vertical format. This is the format that is used to teach and implement the standard algorithm of addition.

The arithmetic expression, 89 + 47, is expressed in a vertical format.

Note how the digits in the one’s column and ten’s column are aligned vertically in this format.

The numbers listed in this format are the addends of the arithmetic expression of addition.

The plus sign, the symbol representing the operation of addition, is placed to the left of the addend at the bottom of the list.

The underline is used to separate the addends from the sum that is about to be calculated. It serves the same function as an equal sign.

When listing the addends associated with the arithmetic expression, the digits associated with the 1s column must line up vertically. The digits associated with the 10s column must also line up vertically. (See the blog “Decimals” for more details). This will make it easier to execute the algorithm properly. All math students should be encouraged to set up these addition problems properly and write them neatly to avoid confusion.

The most common way to gain insights into the validity of algorithms is to express its abstract concepts to the math student in visual concrete ways {visual model}. We’ll explore this concrete model of addition in Part II.

The Mechanical Arithmetic of the Pascaline

Blaise Pascal (1623-1662) is known today as a brilliant French mathematician, physicist, inventor, writer and Christian philosopher. In 1642, he attempted to help his father, a tax collector, deal with the repetitive arithmetic calculations that were part of the task of reorganizing the tax revenues of the French province of Upper Normandy. He was thus motivated to develop and invent the only functional calculator of the 17th century, known as the Pascaline, in 1645. It could add and (indirectly) subtract two numbers. It could also multiply and divide by repetition. In 1649 a royal privilege, by Louis XIV of France, gave him the exclusivity of the design and manufacturing of calculating machines in France. He designed the only functional calculator of the 17th century.

As far as I can tell, nine Pascalines still exist today. Four of them are on display at the National Conservatory of Arts and Crafts (CNAM) museum in Paris, France. There is also an interesting video that explains how this fascinating mechanical calculator worked. I encourage you to watch, learn and explore this intriguing bit of math history and technology.

The Vocabulary of Addition

In order to use language to communicate math concepts and skills concisely {language model}, we must learn the terminology and vocabulary of mathematics so that we can express ourselves accurately. Lets begin by learning the English math words associated with the fundamental skill of addition and its associated numerical expressions {number model}.

An arithmetic expression is a mathematical statement consisting of real numbers and mathematical operations. There are no variables in an arithmetic expression.

The numbers that are being added together are called addends.

The plus sign is the mathematical symbol representing the operation of addition.

The equal sign tells us that the the math statement on its left is the same value (equal) to the math statement on the right

The sum is the value of the addition of the addends.

This arithmetic equation is a mathematical statement which uses the equal sign to state that the arithmetic expression on the left (the sum of the two addends) is equal to the statement on the right of the equal sign (the sum).

Each language and culture uses its own terminology and vocabulary to represent these components of addition. Learning these words and their meaning is one important way the world of language arts and world of mathematics intersects.  One of the most basic tools I use to assess whether a student I am tutoring is fluent in the use of math vocabulary is through the use of flashcards.  I usually just ask the student to identify the component of the expression or equation highlighted in red.  Many times, there is more than one acceptable answer, as you will see in future blogs.

Addition and the Ishango Bone

In today’s blog, we are going to start a steady and cumulative process of exploring the concepts and techniques of mathematics in an evolutionary way. You will soon realize that even the most basic concepts can be seen in different and interesting ways. As always, and whenever possible, I’ll point you to some interesting places, events and people in the history of mathematics.  Lets start with the concept of addition. Addition evolved out of a very fundamental desire to count and know the quantity of similar objects we have.

Suppose we begin with two sets of objects (1). Set A consists of six elements (blue discs) and Set B has three elements (green discs). These two sets have no elements in common. The intersection of sets A and B is the empty set. Thus, they are referred to as disjoint sets. The union of sets A and B consists of both the six blue discs and the three green discs. In the Hindu/Arabic number system, there are numbers that are used to represent the quantities of discs in each set (2). In this case, it is the numbers “6” and “3.” The union of two disjointed sets is a visual way of representing the sum of two numbers. The addition symbol (+) is used to represent the operation of addition in a mathematical expression or equation. The sum of these two numbers is equivalent to counting the number of blue and green discs in the union of two sets (3).  In this case, six plus three is equal to nine.  One should note that counting is nothing more than the repeated addition of 1 to generate a set of natural numbers.

In 1960, a Belgian geologist, Jean de Heinzelin de Braucourt (1920-1998) was exploring an area of Africa near the headwaters of the Nile River at Lake Edwards, called Ishango. At the time, the area was part of the Belgian Congo. He discovered a large number of tools, artifacts, and human remains.  In the world of archeology, there have been numerous discoveries of prehistoric animal bones that have notches carved into them. These artifacts are generally known as tallies or tally sticks. Some of these notched bones have proven to be more interesting to the mathematical community than others. One of these interesting bones was discovered at Ishango by Jean de Heinzelin de Braucourt . Today, this artifact is referred to as the Ishango bone.  It is considered the second oldest mathematical object. However, its exact purpose has yet to be determined.

The Ishango bone is currently on display at the Royal Institute of Natural Sciences in Brussels, Belgium.  There, you will find a Flash-based website on the Ishango archeological site, which will give you a detailed explanation of the bone’s markings and its possible uses. Explore this site and you will find out how far back the history of mathematics stretches.